Summary
This page presents the theoretical basis for using N - 1 rather than N in a chi squared test of a 2 × 2 table or in a comparison of two proportions.
Since the chi squared test was first used as a statistical test of two-by-two tables, the standard procedure has been to compare the formula
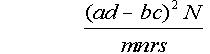
(see nomenclature) against the chi squared distribution with one degree of freedom (Karl Pearson's chi squared test).
However, an alternative formula
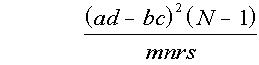
performs better in practice in that Type I errors are a better match to the nominal significance level α. (The only difference in this formula from Karl Pearson's chi squared test is that 'N -1' replaces 'N')
There are theoretical arguments that support the use of this alternative formula. This page detail these arguments.
One way to derive the traditional chi squared formula is by approaching the 2 × 2 table as a pair of proportions, and comparing the difference in the two proportions with the standard error of that difference.
The calculation of the standard error includes the product π (1 - π), where π is the proportion of B in the population (see nomenclature). As π is unknown, it is in some books and articles replaced by p, the observed proportion of B, which is equal to r / N. This means that π (1 - π) is replaced by p(1 - p). This may appear reasonable since p is an unbiased estimate of π.
However, a crucial point is that p(1 - p) is not an unbiased estimate of π (1 - π). Instead, an unbiased estimate is p(1 - p) N / (N - 1). This result is given without proof in Kendall's Advanced Theory of Statistics (see Stuart et al, 1999). A proof of the result follows below.
An unbiased estimate of π (1 - π) is p (1 - p) N / (N - 1)
Where X is a random variable having a binomial distribution with parameters N, π , it will be shown that
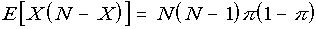
Proof
By definition,
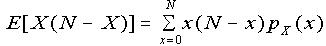
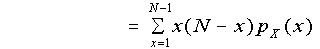
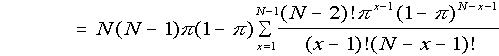
(putting y = x - 1)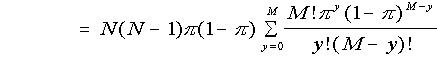
(putting M = N - 2)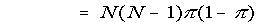
It follows that if p is the observed proportion of B (i.e. p = X / N) then the expectation of
p (1 - p) is π (1 - π) (N - 1) / N,
and an unbiased estimate of π (1 - π) is p (1 - p) N / (N - 1).
Notes
There is an alternative statistical approach to 2 × 2 tables that compares
√[(ad - bc)² N / ( m n r s )] with the normal distribution N(0, 1) , which apart from the square root is identical to the chi squared test. The arguments in favour of 'N -1' replacing 'N' apply just as much to this procedure as to the chi squared test.
References
Stuart A, Ord JK, Arnold S. Kendalls Advanced Theory of Statistics, Vol. 2A, 6th edition. Arnold: London, 1999, p17.
Yates F. Contingency tables involving small numbers and the χ² test. Journal of the Royal Statistical Society Supplement 1934; 1:217-235.
Back to top